 CUET UG Mathematics Answer Key 2024 Unofficial
CUET UG Mathematics Answer Key 2024 UnofficialCUET UG Mathematics Answer Key 2024 Unofficial: The National Testing Agency conducted CUET Mathematics exam 2024 on May 16 from 5:15 PM to 6:15 PM. The candidates who took the Mathematics subject can now check the unofficial answer keys here. CUET Mathematics answer key 2024 for Set A, Set B, Set C and Set D can be checked here along with the detailed question paper analysis. The Mathematics question paper of CUET 2024 consisted of 50 questions out of which 40 questions were to be answered. Each question carries a 5 marks weightage and there is a negative marking of -1 for every wrong attempt. The total marks weightage of the CUET Mathematics is 200 marks.
LATEST (July 7) | CUET UG Answer Key 2024 Released: Response sheet PDF with keys download link
| CUET UG 2024 May 17 Answer Key 2024 | CUET UG Expected Cutoff 2024 for All Subjects |
|---|
CUET UG Mathematics Unofficial Answer Key 2024 (All Sets)
The question-wise answers for the CUET UG Mathematics 2024 can be checked in the table below. The candidates must note that the questions in Sets A, B, C and D will be the same and only the question number changes across different sets . Hence, the questions and answers are directly being added here so that students of all sets can cross-check their answers.
| Question | Answer | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. If A and B are symmetric matrices of the same order, then AB - BA is a : | (3) skew symmetric matrix | ||||||||||
| 2. IIA is a square matrix of order 4 and IA| = 4, then |2A| will be: | (2) 64 | ||||||||||
| 3. If [A] 3×2 [B] x×y = [C] 3×1 , then: | (2) x = 2, y = 1 | ||||||||||
| 4. If a function f(x) = x 2 + bx + 1 is increasing in the interval [1,2], then the least value of b is: | (3) -2 | ||||||||||
| 5. Two dice are thrown simultaneously. If X denotes the number of fours, then the expectation of X will be: | (2) 1/3 | ||||||||||
|
6. For the function f(x) = 2x3 - 9x2 + 12x - 5, x ∈ [0,3], match List-I with List-II:
List-I (A) Absolute maximum value (B) Absolute minimum value (C) Point of maxima (D) Point of minima List-II (I) 3 (II) 0 (III) -5 (IV) 4 Choose the correct answer from the options given below: | (4) (A) - (IV), (B) - (III), (C) - (I), (D) - (II) | ||||||||||
| 7. An objective function Z = ax + by is maximum at points (8, 2) and (4, 6). If a ≥ 0 and b ≥ 0 and ab = 25, then the maximum value of the function is equal to: | (3) 50 | ||||||||||
| 8. The area of the region bounded by the lines x + 2y = 12, x = 2, x = 6 and x-axis is: | (4) 16 sq. units | ||||||||||
| 9. A die is rolled thrice. What is the probability of getting a number greater than 4 in the first and the second theve of dice and a number less than 4 in the third throw? | (4) 1/18 | ||||||||||
|
10. The comer points of the feasible region determined by
x + y ≤ 8, 2x+y ≥ 8, x ≥ 0, y≥ 0 are A(0, 8), (4, 0) and C(8, 0). If the objective function Z = ax + by base its maximum value on the line sept AB, then the relation between a and b is: | (2) a = 2b | ||||||||||
| 11. If t = e 2x and y = log e t 2 , then d 2 y/dx 2 is : | (1) 0 | ||||||||||
| 12. ∫ (π/(x n+1 ) - x) dx = ? | (1) (π/n) log e | (x n - 1)/x n | + C | ||||||||||
| 13. ∫ 0 1 (a - bx 2 ) dx / (a + bx 2 ) 2 = ? | (4) 1/(a + b) | ||||||||||
| 14. The second order derivative of which of the following functions is 5 x ? | (4) 5 x / (log e 5) 2 | ||||||||||
| 15. The degree of the differential equation (1 - (dy/dx) 2 ) 3/2 = k d 2 y/dx 2 | (2) 2 | ||||||||||
| 16. Let R be the relation over the set A of all straight lines in a plane such that l 1 R l 2 ⟷ l 1 is parallel to l 2 . Then R is | (2) An equivalence relation | ||||||||||
| 17. The probability of not getting 53 Tuesdays in a leap year is: | (4) 5/7 | ||||||||||
| 18. The angle between two lines whose direction ratios are propotional <1, 1, -2> and <(√3 - 1), (-√3 - 1), -4> is: | (1) π/3 | ||||||||||
| 19. If (a - b) . (a + b) = 27 and | a | = 2 | b |, then | b | is: | (1) 3 | ||||||||||
| 20. If tan -1 ( 2/(3 -x + 1) ) = cot -1 ( 3/(3 x + 1) ) then which one of the following is true? | (2) There is one positive and one negative real value of x satisfying the above equation. | ||||||||||
| 21. If A, B and C are three singular matrices given by A = [ (1 4), (3 2a)], B = [(3b 5), (a 2)] and C = [(a + b + c c + 1), (a + c c)], then the value of abc is: | (3) 45 | ||||||||||
| 22. The value of integral loge^2 ∫ loge^3 [ (e2x - 1) / (e2x + 1)] dx is: | (2) log e^4 - log e^3 | ||||||||||
| 23. If a, b and c are three vectors such that a + b + c = 0, where a and b are unit vectors and | c | = 2, then the angle between the vectors b and c is: | (4) 180° | ||||||||||
|
24. Let [x] denote the greatest integer function. Then match List-I with List-II:
List-I (A) | x - 1 | + | x - 2 | (B) x - | x | (C) x - { x } (D) x | x | List-Il (I) is differentiable everywhere except at x = 0 (II) is continuous everywhere (III) is not differentiable at x 1 (IV) is differentiable at x = 1 Choose the correct answer from the options given below: | (4) (A) - (II), (B) - (I), (C) - (III), (D) - (IV) | ||||||||||
| 25. The rate of change (in cm 2 /s) of the total surface area of a hemisphere with respect to radius r at r = (1.331) 1/3 cm is | (2) 6.6π | ||||||||||
| 26. The area of the region bounded by the lines x/7√3a + y/b = 4, x = 0 and y = 0 is: | (1) 56√3ab | ||||||||||
| 27. If A is a square matrix and I is an identity matrix such that A 2 = A. then A (I - 2A) 3 + 2A 3 is equal to | (4) A | ||||||||||
|
28. Match List-l with List-II:
List-I (A) Integrating factor of xdy - (y + 2x 2 ) dx = 0 (B) Integrating factor of (2x 2 - 3y ) dx = xdy (C) Integrating factor of (2y + 3x 2 ) dx + xdy = 0 (D) Integrating factor of 2xdy + (3x + 2y) dx=0 List-II (I) 1/x (II) x (III) x 2 (IV) x 3 Choose the correct answer from the options given below: | (2) (A) - (I), (B) - (IV), (C) - (III), (D) - (II) | ||||||||||
|
29. If the function f: N→ N is defined as f(n) = { (n - 1 if is in even), (n + 1 if n is odd), then
(A) f is injective (B) f is into, C) f is surjective (D) f is invertible Choose the correct answer from the options given below: | (4) (A), (C), and (D) only | ||||||||||
| 30. 0 ∫ π/2 [ (1 - cotx) / (cosecx + cosx) ] dx = ? | (1) 0 | ||||||||||
31. If the random variable X has the following distribution :
List-I (A) k (B) P(X < 2) (C) P(X) (D) P(1 ≤ X ≤ 2) List-II (I) 5/6 (II) 4/3 (III) 1/2 (IV) 1/6 Choose the correct answer from the options given below: | (2) (A) - (IV), (B) - (III), (C) - (II), (D) - (I) | ||||||||||
|
32. For a square matrix A
n×n
(A) | adj A | = | A | n-1 (B) | A | = | adj A | n-1 (C) A(adj A) = | A | (D) | A -1 | = 1 / | A | Choose the correct answer from the options given below: | (2) (A) and (D) only | ||||||||||
|
33. The matrix [ (1 0 0), (0 1 0), (0 0 1)] is a:
(A) scalar matrix (B) diagonal matrix (C) skew-symmetric matrix (D) symmetric matrix Choose the correct answer from the options given below: | (1) (A), (B), and (D) only | ||||||||||
34. The feasible region represented by the constraints 4x + y ≥ 80, x + 5y ≥ 115, 3x+2y ≤ 150, x, y ≥ 0 of an LPP is
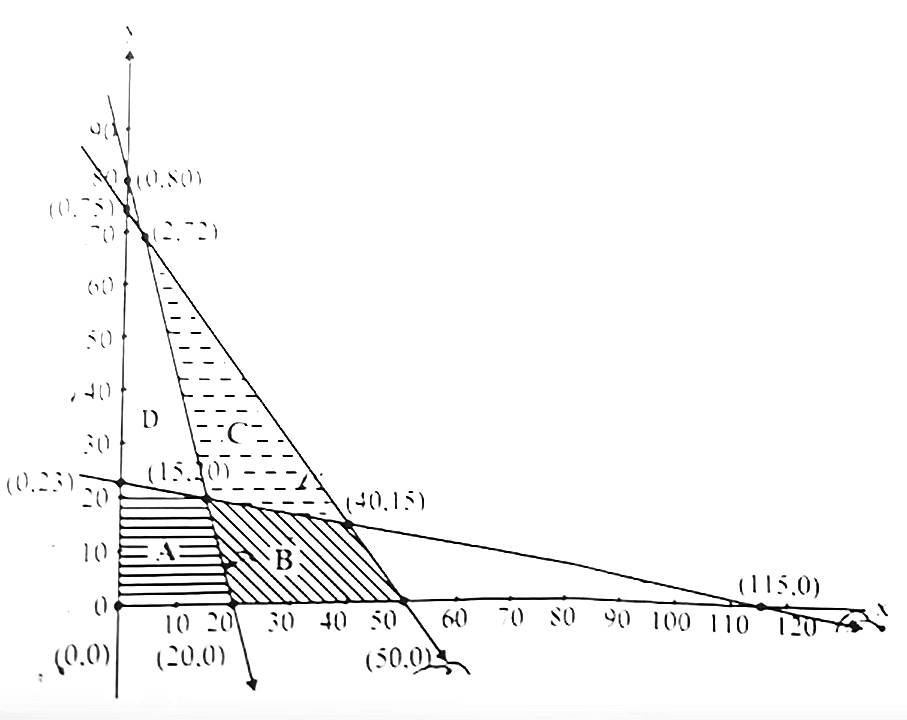 | (3) Region C | ||||||||||
| 35. The area of the region enclosed between the curves 4x 2 = y and y = 4 is: | (4) 16/3 sq. units | ||||||||||
| 36. ∫ e x ( (2x + 1)/(2√x)) dx = ? | (4) e x √x + C | ||||||||||
| 37. If f(x), defined by f(x) = { (kx + 1 if x ≤ π), (cosx if x > π), is continuous at x = π, then the value of k is: | (4) -2/π | ||||||||||
| 38. If P = [(-1), (2), (1)] and Q = [2 -4 1] are two matrices, then (PQ) T will be | (2) [(-2 4 2), (4 8 -4), (-1 2 1)] | ||||||||||
|
39. Δ = | (1, cos x, 1), (- cos x, 1, cos x), (- 1, - cos x, 1) |
(A) Δ = 2(1 - cos 2 x) (B) Δ = 2(2 - sin 2 x) (C) Min value of A is 2 (D) Maximum value of A is 4 Choose the correct answer from the options given below: | (4) (B), (C), and (D) only | ||||||||||
|
40. f(x) = sinx + (1/2)(cos2x) in [0, π/2]
(A) f'(x) = cosx - sin2x (B) The critical points of the functions are x - π/6 and x = π/2 (C)The minimum value of the function is 2 (D) The max value of the function is3/4 Choose the correct answer from the options given below | (1) (A), (B), and (D) only | ||||||||||
| 41. The direction cosines of the line which is perpendicular to the lines with direction ratios 1, -2, -2 and 0, 2, 1 are: | (1) 2/3, -1/3, 2/3 | ||||||||||
|
42. Let X denote the number of hours you play during a randomly selected day. The probability that X can take values & has the following form, where e is some constant.
P(X = x) = { 0.1 if x = 0 { ex if x = 1 or x = 2 { e(5 - x) if x = 3 or x = 4 { 0 otherwise Match List-I with List-II. List-I (A) e (B) P(X ≤ 2) (C) P(X = 2) (D) P(X ≥ 2) List-II (I) 0.75 (II) 0.3 (III) 0.55 (IV) 0.15 Choose the correct answer from the options given below: | (2) (A) - (IV), (B) - (III), (C) - (II), (D) - (I) | ||||||||||
| 43. If sin y = x sin (a - y), then dy / dx is: | (4) sin 2 (a + y) / sina | ||||||||||
| 44. The unit vector perpendicular to each of the vectors a + b and a - b where a = i + j + k and b = i + 2j + 3k is: | (4) (-1/√6)i + (2/√6)j-(1/√6)k | ||||||||||
| 45. The distance between the lines r = i - 2j + 3k - λ (2i + 3j + 6k) and r = 3i - 2j + 1k + μ (4i + 6j + 12k) is: | (3) (√328) / 7 | ||||||||||
|
46. If f(x) = 2 ( tan
-1
(e
x
) - π/4), then f(x) is
(1) even and is strictly increasing in (0, ∞) (2) even and is strictly decreasing in (0, ∞) (3) odd and is strictly increasing in (-∞, ∞) (4) odd and is strictly decreasing in (-∞, ∞) | (3) odd and is strictly increasing in (-∞, ∞) | ||||||||||
|
47. For the differential equation (x log
e
x)dy = (log
e
x - y)dx
(A) Degree of the given differential equation is 1. (B) It is a homogeneous differential equation. (C) Solution is 2y log e x - A = (log e x) 2 , where A is an arbitrary constant (D) Solution is 2y log e x - A = log e (log e x), where A is an arbitrary constant Choose the correct answer from the options given below : | (1) (A) and (C) only | ||||||||||
| 48. There are two bags. Bag-1 contains 4 white and 6 black balls and Bag-2 contains 5 white and 5 black balls. A die is rolled, if it shows a number divisible by 3. a ball is drawn from Bag-1. else a ball is drawn from Bag-2. If the ball drawn is not black in colour, the probability that it was not drawn from Bag-2 is: | (3) 2/7 | ||||||||||
| 49. Which of the following cannot be the direction ratios of the straight line (x - 3)/2 = (2 - y)/3 = (z + 4)/- 1 ? | (3) 2, 3, -1 | ||||||||||
|
50. Which one of the following represents the correct feasible region determined by the following constraints of an LPP?
x + y ≥ 10, 2x - 2y ≤ 25 , x ≥ 0, y ≥ 0 |
(3)
 |
Also read |
| Links |
|---|
| CUET UG Mathematics Expected Cutoff 2024 |
| CUET UG Mathematics Expected Percentile Score 2024 |
CUET Mathematics Question Paper Analysis 2024
The detailed question paper analysis of the CUET Mathematics exam 2024 can be checked in the table below -
| Aspect | Analysis |
|---|---|
| Difficulty Level | Moderate, NCERT-based |
| Topics with Maximum Weightage |
|
| Expected Number of Good Attempts | 32+ questions |
| Was the paper lengthy and time-consuming? | Yes, it was slightly lengthy |
As the exam is being held offline (Pen and Paper) mode, the answer keys will be released online after a few days. Candidates will have the opportunity to raise objections to the answer key online through their login portal, by paying Rs 200 per question. The final answer key will be released after considering the objections raised by the candidates and accordingly, the results will be prepared and released.
| 96 Percentile vs Marks | Expected Marks for 96 Percentile in CUET 2024 |
|---|---|
| 95 Percentile vs Marks | Expected Marks for 95 Percentile in CUET 2024 |
Subject-Wise Answer Keys |
| Subject | Answer Key Link |
|---|---|
| Chemistry | CUET UG Chemistry Answer Key 2024 Unofficial |
| Biology | CUET UG Biology Answer Key 2024 Unofficial |
| English | CUET UG English Answer Key 2024 Unofficial |
| General Test | CUET UG General Test Answer Key 2024 Unofficial |
| Economics | CUET UG Economics Answer Key 2024 Unofficial |
| Hindi | CUET UG Hindi Answer Key 2024 Unofficial |
| Physics | CUET UG Physics Answer Key 2024 Unofficial |


 Follow us
Follow us















